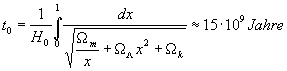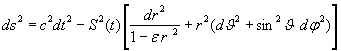Supernovae vom Typ
Ia und Kosmologie
Wir untersuchen hier, welches sehr ernste Problem sich für die Standardkosmologie ergibt, wenn versucht wird, Supernovae vom Typ Ia (SN Ia) als Standardkerzen zu verwenden.
Für die folgenden elementaren Überlegungen zur Krümmung der Kurve im Hubble-Diagramm unterstellen wir einige vereinfachende Voraussetzungen [1]:
1) Der Raum ist euklidisch.
2) Supernovae vom Typ Ia (SN Ia) existierten auch schon zu Beginn des Urknalls. Hierdurch sind sie bis zu diesem Zeitpunkt in der Vergangenheit prinzipiell beobachtbar.
3) Photonen konnten sich bereits unmittelbar nach dem Urknall frei durch das Universum bewegen. Hierdurch ist es möglich, extragalaktische Objekte sowie SN Ia bis hin zum Expansionsbeginn zu beobachten.
4) Photonen bewegen sich immer und überall mit der Lichtgeschwindigkeit c. Hierdurch ergibt sich für jeden Lichtweg D = c * t, wobei t die zugehörige Lichtlaufzeit ist.
5) Die maximal mögliche absolute Helligkeit (absolutes Explosionshelligkeitsmaximum) aller SN Ia hat sich zeitlich nicht entwickelt. Hierdurch können die SN Ia als Standardkerzen betrachtet werden.
6) Der Hubble-Parameter hat heute den Wert H0 = 62,3 km/(Mpc s) [1]. Die Hubble-Zeit beträgt demnach tH = 1/H0 = 15,71 * 109 Jahre = 4,95 * 1017 s (1 Mpc =3,086 * 1024 cm).
Wir wollen nun prüfen, welche Konsequenzen sich aus diesen einfachen Annahmen für die Krümmung von Kurven im Hubble-Diagramm speziell der SN Ia ergeben.
Das Alter (Zeitraum vom Expansionsbeginn bis heute) für ein flaches Universum ergibt sich zu t0 = 2/3 tH = 10,47 * 109 Jahre = 3,3 * 1017 s, wenn eine in der Theorie mögliche Kosmologische Konstante L unberücksichtigt bleibt.
Photonen, die aus der unmittelbaren zeitlichen Nähe des Urknalls zu uns gelangen, haben bis heute einen maximalen Lichtweg Dmax = c * t0 = 9,9 * 1027 cm = 3.208 Mpc zurückgelegt (c = 2,99792458 * 1010 cm/s). Dieser Lichtweg ist verantwortlich für die Abschwächung der Helligkeit der beobachteten Supernovae.
Versetzen wir nun im Rahmen eines Gedankenexperiments eine SN Ia mit der absoluten Maximalhelligkeit Mpeak = -19,49 (peak luminosity, [1]) in die Entfernung Dmax, ergibt sich für diese eine scheinbare Maximalhelligkeit (peak apparent luminosity) gemäß
|
|
(1) |
zu mpeak = 23,04. Wegen der bisher zeitlich begrenzten Lichtlaufzeit t0 und dem zugehörigen Lichtweg können heute noch keine im Vergleich zu diesem mpeak lichtschwächeren SN Ia beobachtet werden (physikalische Effekte, die die scheinbare Helligkeit zusätzlich abschwächen, werden hier nicht berücksichtigt). Außerdem hat es zu Zeiten vor dem Expansionsbeginn (was auch immer das sein mag) noch keine SN Ia gegeben. Genau zu diesem Zeitpunkt t = 0 war der Skalenparameter S(t = 0) aber unendlich klein. Hierdurch ist die zur betrachteten SN Ia mit einer scheinbaren Maximalhelligkeit mpeak gehörende Rotverschiebung z unendlich groß, wie folgender Gleichung sofort zu entnehmen ist:
|
|
(2) |
Die betrachtete SN Ia vom „Rande des Universums“ ist im Hubble-Diagramm demnach nicht eintragbar, weil sie in diesem Diagramm in Richtung der Rotverschiebungsachse im Unendlichen liegt (z = ¥). Alle näheren SN Ia, die zu einem späteren Zeitpunkt explodiert sind, weisen kleinere Rotverschiebungen auf und kommen gewissermaßen aus Richtung z = ¥ entlang der Rotverschiebungsachse in das Hubble-Diagramm hinein. Die Kurve im Hubble-Diagramm krümmt sich deshalb im Rahmen eines expandierenden euklidischen Universums auf jeden Fall von größeren Rotverschiebungswerten kommend zu größer werdenden scheinbaren Helligkeiten hin, wenn immer nähere, d. h jüngere SN Ia betrachtet werden (der Zahlenwert der scheinbaren Helligkeit wird kleiner, die scheinbare Helligkeit selbst nimmt zu). Die gesamte gekrümmte Kurve liegt dabei vor der kleinstmöglichen scheinbaren Helligkeit mpeak!
Außerdem darf jenseits dieses minimalen Grenzwertes der scheinbaren Helligkeit mpeak keine SN Ia gefunden werden, wenn deren absolute Maximalhelligkeit Mpeak tatsächlich im Verlauf der Entwicklung des Universums konstant geblieben ist und sie für alle SN Ia immer denselben Wert hatte, wie es die Theorie der SN Ia fordert. Genau von dieser Voraussetzung macht die heutige Standardkosmologie Gebrauch, die SN Ia als Standardkerzen verwendet.
Anmerkung:
Eine kleinere absolute Maximalhelligkeit Mpeak der SN Ia führt zu einer kleineren scheinbaren Maximalhelligkeiten mpeak. Offenbar ist Mpeak nicht so groß, wie oben angegeben, denn es werden scheinbare Maximalhelligkeiten bis hinunter zu mpeak = 25,517 gemessen (siehe hierzu z.B. [2] bis [7]). Um aber mithilfe von SN Ia wirklich zuverlässig Kosmologie treiben zu können, bedarf es zuvor einer eindeutigen messtechnischen Festlegung der absoluten Maximalhelligkeit Mpeak!
Die Krümmung der Kurve im Hubble-Diagramm in Richtung Rotverschiebungsachse wird durch die zeitliche Entwicklung von S(t) verursacht, weil der Skalenparameter gemäß dem Urknallmodell in der Frühzeit des Universums einmal unendlich klein war. Demnach ist das Urknallmodell (die heutige Standardkosmologie!) falsch, wenn diese Krümmung nicht beobachtet wird. Glauben wir also dem Anspruch, SN Ia als kosmologische Standardkerzen verwenden zu dürfen, wird hierdurch das Urknallmodell selbst widerlegt, weil diese astrophysikalischen Objekte im Hubble-Diagramm nicht die durch den Urknall erforderliche Krümmung der Kurve zeigen! Dieser Umstand wird durch das folgende Bild sehr anschaulich demonstriert, das ein aktuelles Hubble-Diagramm von 52 SN Ia zeigt [8]:
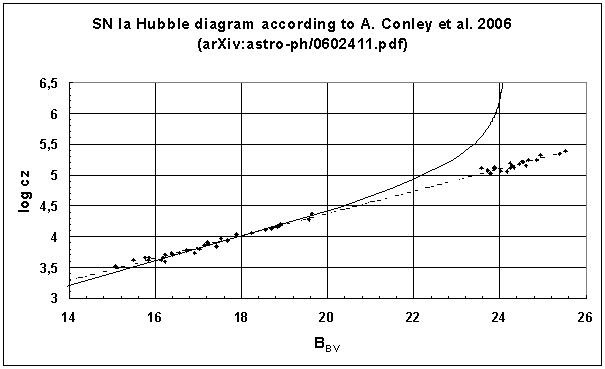
Bild 1
Im Bild 1 ist eine gekrümmte Kurve eingetragen, die den hier vorgestellten qualitativen Argumenten entspricht. Die hierzu vorliegende quantitative Theorie erwartet für Mpeak = -18,4 einen minimalen Grenzwert der scheinbaren Helligkeit mpeak = 24,13. Wenn sich Mpeak der SN Ia mit der Zeit nicht geändert hat und dieser Wert für alle SN Ia stets gleich ist, dürfen unterhalb der gekrümmten Kurve keine SN Ia gefunden werden!
Schauen wir uns zum Vergleich ein Hubble-Diagramm von Quasaren an [9], erkennen wir die durch die obige Argumentation geforderte Krümmung ganz deutlich:
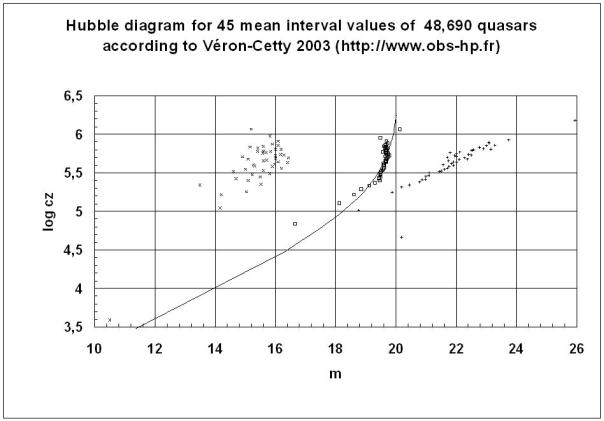
Bild 2
Für die gekrümmte Kurve durch die 45 Intervallmittelwerte gilt eine mittlere absolute Helligkeit der Quasare von MQ = -22,39. Dies führt zu einer mittleren scheinbaren Grenzhelligkeit mgrenz = 20,14 für diese extragalaktischen Objekte.
Die Kreuze links im Bild markieren die jeweils lichtstärksten Quasare im Intervall, während die Pluszeichen rechts im Bild die jeweils lichtschwächsten Quasare repräsentieren. Interessant ist hier, dass sich die lichtschwächsten Quasare in etwa auf einer geraden Linie verteilen.
Auch nach der auf dieser Homepage dargestellten Theorie werden Quasare keinesfalls als Standardkerzen betrachtet, weil deren absolute Helligkeiten ganz offensichtlich über einen sehr weiten Bereich streuen. Dennoch ist die Rotverschiebung der Quasare ein eindeutiger Entfernungsindikator!
Nun gehen wir noch der Frage nach, ob sich die obigen Schlussfolgerungen verändern, wenn wir die aktuell diskutierte Version vom sich beschleunigt ausdehnenden Universum in Betracht ziehen.
In diesem Fall ist das Universum ebenfalls euklidisch, aber die Kosmologische Konstante L ist ungleich null. Für das Alter des Universums ergibt sich dann (siehe hierzu z. B. [10]):
|
|
(3) |
Die dimensionslose Größe x ist der Quotient aus dem
zeitabhängigen Skalenparameter S(t) und seinem heutigen Wert S(t0). Die dimensionslosen W-Parameter beschreiben die heutige Materiedichte rm, die Dichte der
Dunklen Energie rL und die „Krümmungsdichte“ rk, in ihrer jeweils
auf die kritische Dichte rkr genormten Form:
|
|
(4a) |
und
|
|
(4b) |
und
|
|
(4c) |
Die kritische Dichte berechnet
sich zu
|
|
(5) |
Für ein euklidisches Universum ist
rk = Wk = 0 anzusetzen.
Das angegebene Weltalter folgt numerisch aus den messtechnisch ermittelten Parameterwerten
(Wm; WL; Wk; q0) = (0,3; 0,7; 0; -0,5) und H0 = 62,3 km /(s Mpc).
Hier ist q0 der heutige Verzögerungsparameter und H0 der aktuelle Hubble-Parameter. Es zeigt sich, dass im Fall einer nichtverschwindenden Kosmologischen Konstante das Weltalter t0 mit der Hubble-Zeit tH vergleichbar ist.
Ein Photon kann im Universum nicht länger unterwegs gewesen sein, als es das Weltalter t0 angibt. Rechnen wir die 15 * 109 Lichtjahre in Mpc um, ergibt sich D0 = 4.599 Mpc (1 Lj = 0,3066 pc). Eine SN Ia in dieser Entfernung erscheint uns gemäß Gleichung (1) mit einer scheinbaren Helligkeit von mpeak = 23,82, wenn wir wieder Mpeak = -19,49 annehmen. Für das Hubble-Diagramm der SN Ia bedeutet dies, dass sich die Kurve spätestens in der Nähe von m = 23 anfangen muss ganz stark in Richtung Rotverschiebungsachse zu krümmen, um der theoretischen Erwartung eines Urknalls mit anschließender Expansion gemäß der Friedmann-Gleichung zu genügen. Das Bild 1 zeigt aber ganz deutlich, dass die erwartete Krümmung der Kurve nicht annähernd realisiert ist. Hierdurch ist die obige Argumentation auch für den Fall der zurzeit favorisierten Möglichkeit einer nichtverschwindenden Kosmologischen Konstante gültig.
***************************************************************************
Anhang:
Im Rahmen der Standardkosmologie werden Photonen im Universum durch das Nullsetzen des Linienelementes ds der Robertson-Walker-Metrik (RWM)
|
|
(6) |
beschrieben, wodurch sich eine einfache Gleichung für den euklidischen Raum (e = 0) ergibt:
|
|
(7) |
Auf der linken Seite der Gleichung steht die konstante Lichtgeschwindigkeit c, also eine echte physikalische Größe. Auf der rechten Seite der Gleichung befindet sich der zeitabhängige Skalenparameter S(t) im Produkt mit der Änderungsgeschwindigkeit dr/dt der mitbewegten Radialkoordinate r. Dies drückt aus, dass sich die mitbewegte Radialkoordinate für Photonen während ihrer Reise durch das Universum ändert. Das bedeutet, dass sich die Photonen von einem extragalaktischen Objekt am Ort r1 zum anderen Objekt am Ort r2 bewegen, während diese extragalaktischen Objekte ihren jeweils angestammten mitbewegten Ort r nicht verlassen (für sie gilt r = const !). Weil S(t) in einem expandierenden Universum gemäß der Friedmann-Gleichung wächst, muss für Photonen dr/dt mit der Zeit kleiner werden, damit Gleichung (7) immer erfüllt wird. Die offensichtliche Interpretation dieser Gleichung ist demnach, dass die Photonen im Verlauf der Zeit zwar immer langsamer von einem mitbewegten radialen Koordinatenort r zum anderen vordringen können, sie sich aber dennoch in Summe stets mit Lichtgeschwindigkeit bewegen, weil die sinkende Geschwindigkeit dr/dt durch den mit der Zeit wachsenden Skalenparameter immer gerade so kompensiert wird, dass die Gleichung (7) gültig bleibt. Demnach bewegen sich die Photonen auch gemäß der RWM immer mit der physikalischen Lichtgeschwindigkeit c durch das Universum.
Im Zusammenhang mit der Gleichung (7) existiert aber ein weiteres ernstes Problem:
In der RWM ist r als zeitlich konstant zu betrachten (mitbewegte Koordinate für alle Galaxien)! Nur unter dieser Bedingung ergibt sich aus den Einsteinschen Feldgleichungen die bekannte Friedmann-Gleichung, d.h. die Grundgleichung der Kosmologie. Durch das Nullsetzen des Linienelementes der RWM wird r zu einer zeitabhängigen Größe, was der Grundvoraussetzung der RWM widerspricht. Das bedeutet, dass dieses Nullsetzen genaugenommen nicht zulässig ist, dass die Bewegung der Photonen demnach nicht durch Gleichung (7) beschrieben werden kann und die obige Interpretation der Gleichung deshalb falsch ist.
Weil mithilfe dieser Nullsetzung auch die Gleichung (2) abgeleitet wird (siehe hierzu die einschlägigen Lehrbücher über Allgemeine Relativitätstheorie bzw. Kosmologie), muss auch an deren Richtigkeit gezweifelt werden.
Literatur:
[2] L. Perivolaropoulus, arXiv:astro-ph/0601014.pdf
[3] P. Astier et
al., arXiv:astro-ph/0510447.pdf
[4] A.V. Filippenko
et al., arXiv:astro-ph/9807008.pdf
[5] J. L. Tonry
et al., arXiv:astro-ph/0305008.pdf
[6] A.V. Filippenko, arXiv:astro-ph/0309739.pdf
[7] S. Nobili et al., arXiv:astro-ph/0504139.pdf
[8] A. Conley et
al., arXiv:astro-ph/0602411.pdf
[9]
Véron-Cetty, M.-P. und Véron, P.:
"A Catalogue of Quasars and Active Nuclei", 9th
edition, March 2000, http://www.obs-hp.fr
[10] T. Fließbach: „Allgemeine Relativitätstheorie“, 4. Auflage, ab Seite 320
Copyright
by Steffen Haase, Leipzig (2006)
Letzte inhaltliche Änderung: 24.12.2006
Letzte Schreibfehlerkorrektur: 24.12.2006